Cryptographic signatures in Bitcoin

Introduction

This blog describes at a technical level how Ellyptic Curve Cryptography (ECC) is used for signing Bitcoin transactions. Caveat emptor: I am not a mathematician let alone a cryptographer. I created this document mainly for helping myself understand how ECC is applied and welcome any correction on errors present in this blog. Other criticism is welcomed as well. Please direct feedback to me via email or Twitter. This site is a static site and I haven't yet bothered to install a proper (stateless) commenting system.

Discrete logarithms

ECC, at least as applied to signatures in Bitcoin, is akin to the Discrete Logarithm (DL) problem, so I'll briefly introduce that. The idea is that it is easy to calculate a base number to the power of an exponent modulo some prime, but given the result it is extremely hard to calculate what number was used as the exponent. As an example:
\( 26^{41} \pmod{127} = 9 \)
but given 26, 127 and 9, the only way to find the value 41 is using brute force. Here the number 41 is the "private key" and the combination of 26, 127 and 9 is the "public key". This is an example with small numbers but in reality the prime, exponent and base are in the order of a 617-digit number or more. The numbers should be this large because there is a slightly better algorithm than brute force to find the exponent, called "Number field sieve".

Ellyptic curve operations

In ECC, operations are done with points on an ellyptic curve. The curve that is used in Bitcoin (as well as the standard curve that is used for TLS) is called a "Weierstrass curve" and in short form it has an equation like \( y^2 = x^3 + ax +b \) where \( a\) and \( b\) are some constant. The curve used in Bitcoin has a value for \( a\) of 0 and a value for \( b\) of 7, so the curve is \( y^2 = x^3 + 7 \). The images in this blog are based on that curve.

There are other curve types used in cryptography, like "Edwards curves" and "Montgomery curves" but their discussion is out of the scope of this article. The famous "curve 25519" from Dan Bernstein that is used quite a lot these days is an example of a Montgomery curve.

In Weierstrass curves, "adding" two points means drawing a line through the two points, finding a third point where this line crosses the curve and reflecting that point on the X axis (see image). The reflecting is the ECC way of getting the "negative" point, so in the image where the line crosses the curve is "\( -(P+Q)\)" and the reflection is "\(P+Q\)". This rather strange operation has the effect that some standard group operations apply. So \( A+B = B+A\) and \( A+(B+C) = (A+B)+C\).

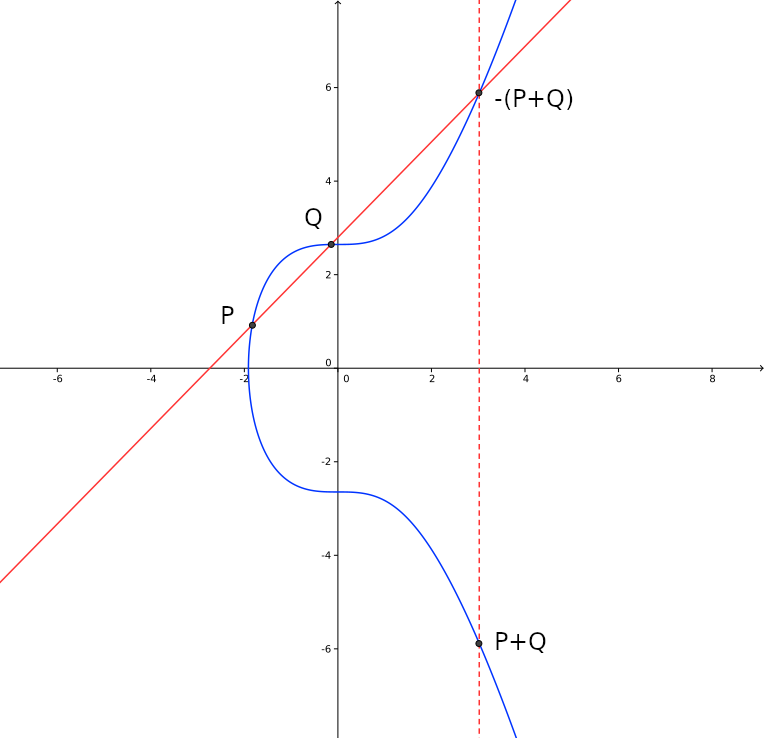
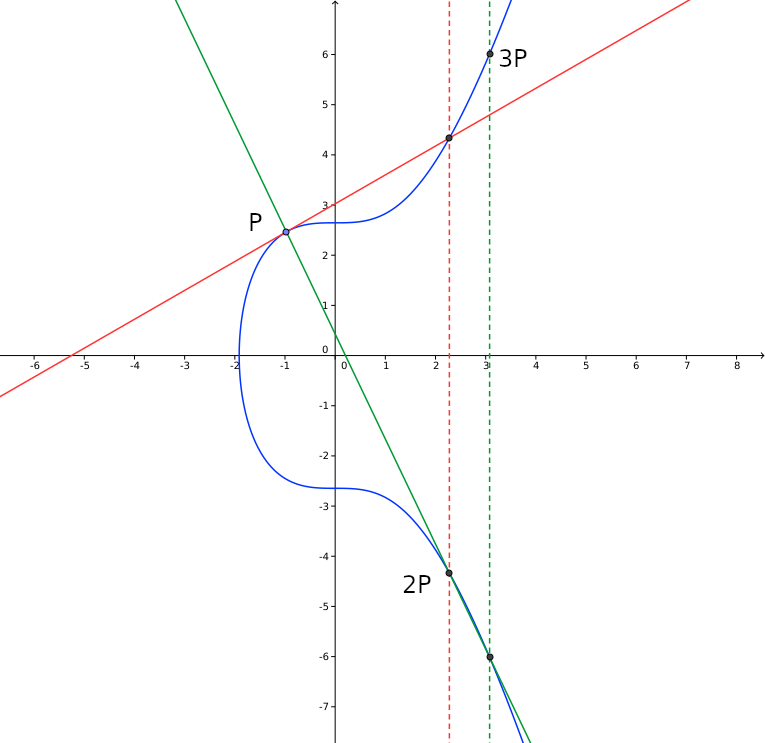
Doubling a point means taking the tangent line to the curve in that point, finding the cross point and reflecting that. Multiplying a point with a value means repeatedly adding the point to itself (see next image where we multiply the point \( P\) with the value \( 3\) by first doubling \(P\) and adding the result to \(P\).

Ellyptic curve operations modulo primes

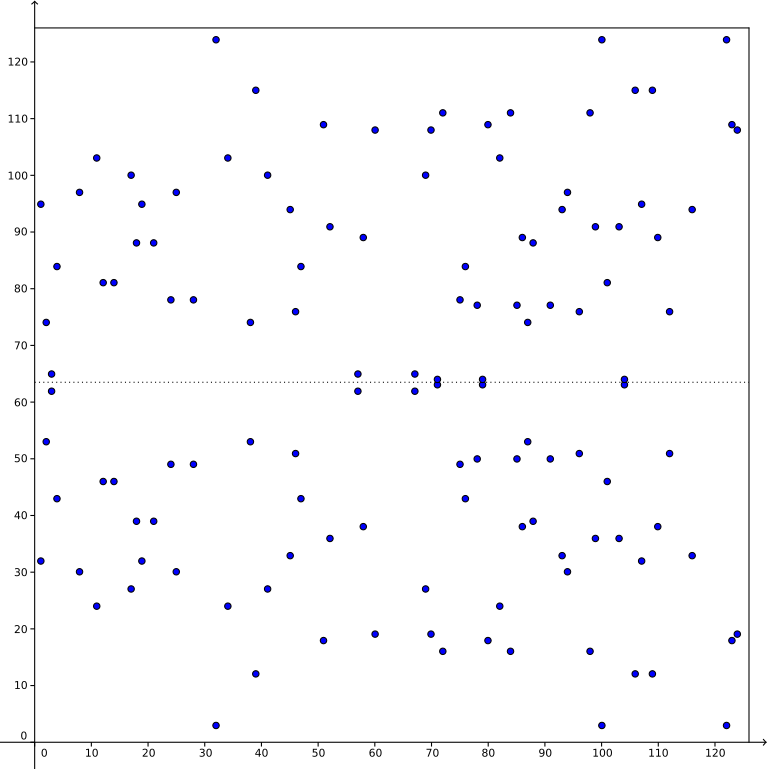
To do ECC, we take the rational values on the curve (i.e., the curve points where each coordinate can be expressed as a division of two integers) and calculate those values modulo some prime \( p\). About the only thing that is still recognizable is the vertical symmetry, which makes sense. If point \(A\) is a rational point on the curve, then so point is \(-A\).

Given the rational points modulo \(p\), one or more groups emerge such that using any point in that group, multiplying that point by the integers from 1 to the group size yields all points in the group. In the image below we have the rational points for \( y^2=x^3+7\) modulo 127. The group size is 126 so any of these points can be used as a "generator" for the group.

Even though the dots do not seem to resemble the curve we saw above, the mechanism for adding points still works (as does point doubling but there the slope of the line is not as obvious). In the image below we add the points \((38,53)\) and \((67,65)\) to get the result, i.e. \((19,95)\).

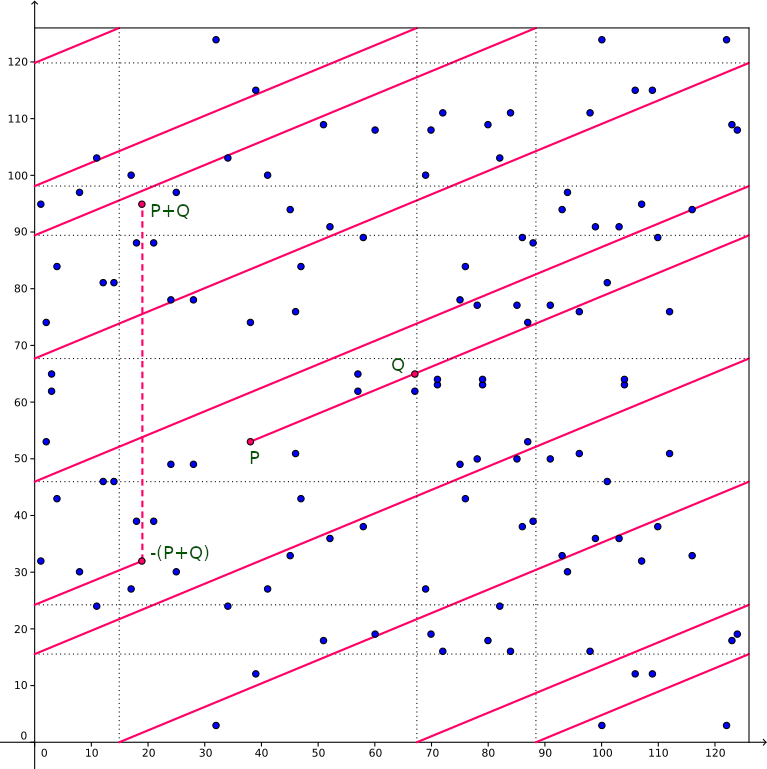
Note that in integer operations modulo a prime \( p\), calculating $\frac{a}{b}$ means finding a value \(c\) such that \( b \times c = 1 \pmod{p}\) (using the Extended Euclidean Algorithm) and then calculating $a\times c$.

To add two points \( (r_1, r_2)\) and \( (s_1, s_2)\), you calculate:

\begin{aligned} \lambda &= ( \frac{s_2-r_2}{s_1-r_1} ) \pmod{p} \\ x &= ( {\lambda}^2 - r_1 - r_2 ) \pmod{p} \\ y &= ( \lambda (r_1 - x) - r_2 ) \pmod{p} \end{aligned}

To double a point \( (r_1, r_2)\) you calculate:

\begin{aligned} \lambda &= ( \frac{3{r_1}^2+a}{2r_2} ) \pmod{p} \\ x &= ( {\lambda}^2 - 2r_1 ) \pmod{p} \\ y &= ( \lambda (r_1-x)-r_2 )\pmod{p} \\ \end{aligned}

The value \(a\) is the from the curve formula \(y^2=x^3+ax+b\). In our case it has the value 0.

The discrete log problem can be translated as, given an integer \(q\), a generator point \(G\) and a prime modulus \(p\), it is easy to calculate the curve point \(Q\) such that \(Q = q\cdot G \pmod{p}\), but given \(Q\), \(G\) and \(p\) is it infeasible to calculate \(q\).

After more than three decades of crypt-analysis, no equivalent of the "number field sieve" has been found for ECC, so the numbers can be a lot smaller. A prime of 256 bits (77 digits) is very common and considered secure with classic computing.

DSA and ECDSA

Note: when describing the various signature algorithms I'll use the addition and multiplication representation as used in ECC instead of the multiplication and exponentiation system as used in discrete logarithms. For getting the point across it should not matter.

In 1989 Claus Schnorr developed an efficient algorithm to create digital signatures based on the discrete log problem. He patented the algorithm (which expired in 2008) so the NSA developed another (less efficient) algorithm which became the de facto standard, named DSA. ECSDA is the equivalent of DSA using curve points, which we describe here.

The following notation is used from here on:

• \( G \):$\phantom{A}$ Generator point on the curve
• \( a \):$\phantom{A}$ (lowercase character): integer
• \( A \):$\phantom{A}$ (uppercase character): curve point
• \( \mathtt{H}() \):$\phantom{A}$ hash function
• \( \mathbf{M} \):$\phantom{A}$ signed message
• \( \Vert{} \):$\phantom{A}$ concatenation

Signature creation

\begin{aligned} x &\leftarrow \{1..n\}\phantom{A}\text{(integer, private key, n is group size)} \\ X &= x \cdot G \phantom{A}\text{(public key)} \\ r &\leftarrow \{1..n\}\phantom{A}\text{(nonce, random integer)} \\ (k,y) &= r \cdot G \phantom{A}\text{(use only the x coordinate)}\\ z &= \mathtt{H}(\mathbf{M}) \\ s &= \frac{z+kx}{r} \\ \end{aligned}

Signature: \( (k,s) \)

Signature verification

\begin{aligned} &\frac{z}{s} \cdot G + \frac{k}{s} \cdot X \Leftrightarrow \\ &\frac{z+kx}{s} \cdot G \Leftrightarrow \\ &\frac{(z+kx)\cdot r}{z+kx} \cdot G \Leftrightarrow \\ &r \cdot G \\ &(k_v, y) = r \cdot G \end{aligned}

Verifies if \(k_v\) is equal to \(k\)

It is important that the nonce is unique for each signature. If it is known that the same nonce is reused for multiple messages, the private key is exposed like this:

\begin{aligned} &s = \frac{z+kx}{r} \\ &s' = \frac{z'+kx}{r} \\ &\frac{sz'-s'z}{k(s'-s)} \Leftrightarrow \\ &\frac{r(zz'+kxz'-z'z - kxz)}{r(kz'-kz)} \Leftrightarrow \\ &\frac{x(kz'-kz)}{kz'-kz} \Leftrightarrow x \end{aligned}

To tackle this, RFC6979 was created to create a deterministic nonce which dependends on the message \(\mathbf{M}\).

A second problem with ECDSA is malleability. Because only the X coordinate of the point \(r\cdot G\) is used, the negative value of the signature is also a valid signature. Before the introduction of the SegWit protocol change in Bitcoin, the signature was used as part of the transaction id. By modifying the signature this way a different transaction id can be generated by someone without the private key. Remember that the negative value of a curve point is its reflection on the X axis. The malleability is pretty obvious. If you do the verification steps with \((k,-s)\) you end up with the curve point \(-r\cdot G\) which is the same as \(-(r\cdot G)\) which is the reflection of the original point on the X axis, thus having the same X coordinate (\(k\)).

Schnorr signatures

With the activation of Taproot in 2021, a few new mechanisms were introduced in the Bitcoin consensus protocol, one of which is Schnorr signatures. This is the original signature algorithm by Claus Schnorr which is now patent free. The algorithm is quite a bit simpler than ECDSA:

Signature creation

\begin{aligned} x &\leftarrow \{1..n\}\phantom{A}\text{(integer, private key, n is group size)} \\ X &= x \cdot G \phantom{A}\text{(public key)} \\ r &\leftarrow \{1..n\}\phantom{A}\text{(nonce, random integer)} \\ R &= r\cdot G \\ q &= \mathtt{H}(\mathbf{M}\Vert{}R) \\ s &= r - qx \end{aligned}

Signature: \( (q,s) \)

Signature verification

\begin{aligned} R_v &= s \cdot G + q \cdot X \\ &= r \cdot G - qx \cdot G + qx \cdot G \\ &= r\cdot G \\ q_v &= \mathtt{H}(\mathbf{M}\Vert{}R_v) \end{aligned}

Verifies if $q_v$ is equal to \(q \)

One advantage of Schnorr signatures is it's linearity. You can tweak the public key and signature with an integer value and the signature still validates:

\begin{aligned} X'&=n\cdot X \\ s'&=r-qnx\\ R_v &= s'\cdot G + q\cdot X'\\ &= r\cdot G -qnx\cdot G+qnx\cdot G \end{aligned}

This is used by Taproot where alternative spending conditions are encoded in a Merkalized Abstract Syntax Tree and the Merkle Root hash is used as a tweak value on the primary spending key.

As with ECSDA, the nonce should be unique for every signature, because reusing the nonce reveals the private key:

\[\frac{s'-s}{q-q'} = \frac{r-q'x -r+qx}{q-q'} = \frac{x(q-q')}{q-q'}\]

MuSig

The linearity of Schnorr signatures enables adding public keys and singatures together so that a n-of-n multisig can be represented as a single signature on a single public key. Simply adding the public keys together poses a risk though. A bad actor could wait for all other public keys to be posted and subtract them from his own public key, adding this modified key to the mix. The result is that the "aggregate" key will be only his own public key so he has sole control of signing a transaction on what was assumed to be a n-of-n multisig. To thwart this, Greg Maxwell et al developed MuSig which requires some collaboration.

Signature creation

\begin{aligned} x_i &\leftarrow \{1..n\}\phantom{A}\text{(integer, private key for user i)} \\ X_i& = x_i \cdot G \phantom{A}\text{(public key for user i)} \\ l &= \mathtt{H}(\sum_i{X_i}) \phantom{A}\text{(the hash of all public keys added together)} \\ t_i &= \mathtt{H}(l\Vert{}X_i) \\ X &= \sum_i{(t_i\cdot X_i)} \\ &= (\sum_i{(t_i{}x_i)})\cdot G \\ r_i &\leftarrow \{1..n\}\phantom{A}\text{(nonce, random integer)} \\ R_i &= r_i \cdot G \\ R &= \sum_i{R_i} \\ &= (\sum_i{r_i})\cdot G \\ q &= \mathtt{H}(X\Vert{}R\Vert{}\mathbf{M}) \\ s_i &= r_i + q{}x_i{}t_i \\ s &= \sum_i{s_i} \\ &= \sum_i{r_i}+q\cdot\sum_i{(x_i{}t_i)} \\ \end{aligned}

Signature: \( (q,s) \)

Signature verification

\begin{aligned} R_v &= s \cdot G - q\cdot X \\ q_v &= \mathtt{H}(X\Vert{}R_v\Vert{}\mathbf{M}) \\ \end{aligned}

Verifies if \(q_v\) is equal to \(q\)

MuSig in itself is not part of the Bitcoin consensus protocol, apart from how \(q\) is calculated, i.e., the hash includes the (possibly aggregate) public key. In the original Schnorr signature this was not included. From the verifier's perspective, the signature verification is the same for a simple Schnorr signature or a MuSig signature, which is exactly the purpose of MuSig.

The fact that it isn't part of the consensus protocol means that other signature protocols can be used, as long as the verification algorithm is identical to the one above. Two such algorithms have already been proposed to tackle the fact that MuSig requires three interactive rounds of communication between participants and that the deterministic nonces as described in RFC6979 cannot be applied safely because due to the multi-round nature of the protocol a participant can be tricked into signing different messages with the same nonce via a replay attack (where part of the interactive communication is redone). The first of these protocols tackles the deterministic nonce and is named MuSig-DN. It uses a special hash algorithm called Purify on the message, all participating public keys and a special nonce key to generate both the nonce and a zero knowledge proof to prevent the nonce to be changed between rounds. The number of rounds is reduced to two but the protocol is still interactive. The second protocol is called MuSig2 which reduces the number of rounds to two, one of which can be precomputed and with that, create a non-interactive MuSig protocol.